Da Vinci Firmware 1
Firmware for the DaVinci-M rocket avionics board.
Loading...
Searching...
No Matches
Functions
optimalAngle.h File Reference
Core Flight Logic » Control Algorithms

Model Predictive Controller (MPC) to determine the optimal airbrake angle. More...

#include "rtwtypes.h"
#include <stddef.h>
#include <stdlib.h>
Include dependency graph for optimalAngle.h:
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions

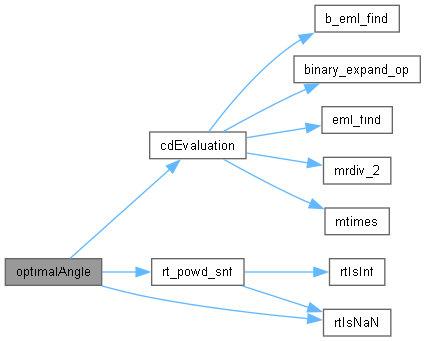
double optimalAngle (double sim_time_step, double altitude, double temperature, double velocity, double pressure, double current_delta, double tilt_angle, double target_apogee, double tolerance, const double mach_states[5], const double deployment_states[6], const double cd_table[30])
 Calculates the optimal constant airbrake angle to reach a target apogee.
 

Detailed Description

Model Predictive Controller (MPC) to determine the optimal airbrake angle.

Author
Francesco Abate, MSA (Originally generated by MATLAB Coder)
Version
24.2 (MATLAB Coder version)
Date
2025-05-06

This header file declares the optimalAngle function, which is the core of the rocket's Model Predictive Control (MPC) system for apogee control. Its primary goal is to calculate the single, constant airbrake deployment angle that, if applied from the current moment, will result in the rocket reaching a specified target apogee.

The function uses a combination of two main algorithms:

  1. Binary Search (Bisection Method): An outer loop efficiently searches for the optimal angle within a defined range [0, 173 degrees].
  2. Trajectory Simulation: For each test angle from the binary search, an inner loop simulates the rocket's entire coasting phase using a physics model and numerical integration (Heun's method) to predict the resulting apogee.

This function was generated from a MATLAB model provided by the MSA subteam.

Definition in file optimalAngle.h.

Function Documentation

◆ optimalAngle()

double optimalAngle ( double  sim_time_step,
double  altitude,
double  temperature,
double  velocity,
double  pressure,
double  current_delta,
double  tilt_angle,
double  target_apogee,
double  tolerance,
const double  mach_states[5],
const double  deployment_states[6],
const double  cd_table[30] 
)

Calculates the optimal constant airbrake angle to reach a target apogee.

Parameters
[in]sim_time_stepThe duration of a single time step used inside the internal trajectory simulation, in seconds (s).
[in]altitudeThe rocket's current altitude above ground level in meters (m).
[in]temperatureCurrent ambient air temperature in Kelvin (K).
[in]velocityThe rocket's current total speed (magnitude of velocity vector) in m/s.
[in]pressureCurrent ambient air pressure in Pascals (Pa).
[in]current_deltaThe current, real-world deployment angle of the airbrakes in degrees. (Note: May not be used in this version).
[in]tilt_angleThe angle of the rocket's velocity vector with respect to the vertical axis in radians.
[in]target_apogeeThe desired final apogee for the rocket in meters (m).
[in]toleranceThe desired precision for the binary search, in degrees. The search stops when dep_max - dep_min <= tolerance.
[in]mach_statesAn array of 5 discrete Mach numbers that form the x-axis of the Cd lookup table.
[in]deployment_statesAn array of 6 discrete airbrake deployment angles that form the y-axis of the Cd lookup table.
[in]cd_tableA 1D array of 30 Coefficient of Drag (Cd) values, representing the 6x5 lookup grid (row-major).
Returns
The calculated optimal airbrake deployment angle in degrees.

Definition at line 86 of file optimalAngle.c.

92{
93 double dep_max;
94 double dep_min;
95 double max_change;
96 double opt_dep;
97 /* placeholder */
98 dep_min = 0.0;
99 /* deg */
100 dep_max = 173.0;
101 /* deg */
102 max_change = 182.6 * sim_time_step;
103 while (dep_max - dep_min > tolerance) {
104 double delta;
105 double elapsed_time;
106 double pressure_current;
107 double temperature_current;
108 double test_delta;
109 double v_current;
110 double x_dot_predicted;
111 double y_current;
112 double y_dot_current;
113 test_delta = (dep_max + dep_min) / 2.0;
114 delta = current_delta;
115 elapsed_time = 0.0;
116 temperature_current = temperature;
117 pressure_current = pressure;
118 y_current = altitude;
119 v_current = velocity;
120 x_dot_predicted = velocity * sin(tilt_angle);
121 y_dot_current = velocity * cos(tilt_angle);
122 while (y_dot_current > 0.0) {
123 double speed_of_sound;
124 double x_dotdot;
125 double y_dotdot;
126 if (elapsed_time > 0.1) {
127 opt_dep = test_delta - delta;
128 if (fabs(opt_dep) > max_change) {
129 if (rtIsNaN(opt_dep)) {
130 opt_dep = rtNaN;
131 } else if (opt_dep < 0.0) {
132 opt_dep = -1.0;
133 } else {
134 opt_dep = (opt_dep > 0.0);
135 }
136 delta += opt_dep * max_change;
137 } else {
138 delta = test_delta;
139 }
140 }
141 speed_of_sound = sqrt(401.79999999999995 * temperature_current);
142 pressure_current = 0.5 *
143 (pressure_current / (287.0 * temperature_current)) *
144 0.014102609421964583;
145 opt_dep = pressure_current * cdEvaluation(deployment_states, mach_states,
146 cd_table, delta,
147 v_current / speed_of_sound);
148 x_dotdot = -opt_dep * x_dot_predicted * v_current / 23.458000008756152;
149 y_dotdot =
150 -opt_dep * y_dot_current * v_current / 23.458000008756152 - 9.81;
151 opt_dep = x_dot_predicted + x_dotdot * sim_time_step;
152 temperature_current = y_dot_current + y_dotdot * sim_time_step;
153 v_current =
154 sqrt(opt_dep * opt_dep + temperature_current * temperature_current);
155 opt_dep = pressure_current * cdEvaluation(deployment_states, mach_states,
156 cd_table, delta,
157 v_current / speed_of_sound);
158 x_dot_predicted += 0.5 *
159 (x_dotdot + -opt_dep * x_dot_predicted * v_current /
160 23.458000008756152) *
161 sim_time_step;
162 opt_dep =
163 y_dot_current + 0.5 *
164 (y_dotdot + (-opt_dep * y_dot_current *
165 v_current / 23.458000008756152 -
166 9.81)) *
167 sim_time_step;
168 y_current += 0.5 * (y_dot_current + opt_dep) * sim_time_step;
169 y_dot_current = opt_dep;
170 v_current = sqrt(x_dot_predicted * x_dot_predicted + opt_dep * opt_dep);
171 temperature_current = temperature - 0.00649 * (y_current - altitude);
172 pressure_current =
173 pressure * rt_powd_snf(temperature_current / temperature, 5.2561);
174 elapsed_time += sim_time_step;
175 }
176 if (y_current > target_apogee) {
177 dep_min = test_delta;
178 } else {
179 dep_max = test_delta;
180 }
181 }
182 return 180 - ((dep_min + dep_max) / 2.0);
183}
cdEvaluation
double cdEvaluation(const double dep_states[6], const double mach_states[5], const double cd_table[30], double dep, double mach)
Estimates the coefficient of drag (Cd) via 2D bilinear interpolation.
Definition cdEvaluation.c:30
rtIsNaN
boolean_T rtIsNaN(real_T value)
Checks if a double-precision value is Not-a-Number (NaN).
Definition rt_nonfinite.c:60
rtNaN
real_T rtNaN
Global constant for Not-a-Number (double precision).
Definition rt_nonfinite.c:24
current_delta
double current_delta
Definition main.c:257
mach_states
const double mach_states[]
Definition main.c:261
altitude
float_t altitude
Definition main.c:224
tilt_angle
double tilt_angle
Definition main.c:260
sim_time_step
double sim_time_step
Definition main.c:256
tolerance
double tolerance
Definition main.c:259
velocity
float_t velocity
Definition main.c:225
target_apogee
double target_apogee
Definition main.c:258
deployment_states
const double deployment_states[]
Definition main.c:262
cd_table
static double cd_table[]
Definition main.c:263
rt_powd_snf
static double rt_powd_snf(double u0, double u1)
Definition optimalAngle.c:27

References altitude, cd_table, cdEvaluation(), current_delta, deployment_states, mach_states, rt_powd_snf(), rtIsNaN(), rtNaN, sim_time_step, target_apogee, tilt_angle, tolerance, and velocity.

Referenced by StartMPC_Task().

Here is the call graph for this function:
Here is the caller graph for this function: