kalmanFilter.c File Reference

#include "kalmanFilter.h"
#include "mrdivide_helper.h"
#include <math.h>

Include dependency graph for kalmanFilter.c:

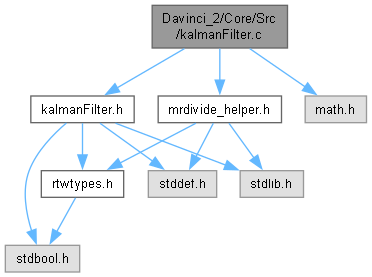
Go to the source code of this file.

Functions
void	kalmanFilter (double x_est[2], double P[4], const double z[2], double alpha, double a_m, double Ts, const double Q[4], const double R[4], bool gnss_signal)
	Executes one prediction and correction step of the Kalman filter.

Function Documentation

kalmanFilter()

void kalmanFilter	(	double	x_est[2],
		double	P[4],
		const double	z[2],
		double	alpha,
		double	a_m,
		double	Ts,
		const double	Q[4],
		const double	R[4],
		bool	gnss_signal
	)

Executes one prediction and correction step of the Kalman filter.

Parameters

[in,out]	x_est	State Estimate Vector [2x1]. On input, the previous state; on output, the updated state. x_est[0]: Altitude in meters (m). x_est[1]: Vertical velocity in meters per second (m/s).
[in,out]	P	Estimate Covariance Matrix [2x2]. Represents the filter's uncertainty. Updated in place. Stored as a 4-element row-major array.
[in]	z	Measurement Vector [2x1]. Raw sensor readings. z[0]: Measured altitude from barometer (m). z[1]: Measured vertical velocity from GNSS (m/s).
[in]	alpha	The rocket's tilt angle (angle from vertical) in radians. Used to project acceleration.
[in]	a_m	Measured longitudinal acceleration (along the rocket's body axis) in m/s^2.
[in]	Ts	The time step (delta time) since the last filter update in seconds (s).
[in]	Q	Process Noise Covariance Matrix [2x2]. Models the uncertainty of the physics prediction. Stored as a 4-element row-major array.
[in]	R	Measurement Noise Covariance Matrix [2x2]. Models the sensor noise. Stored as a 4-element row-major array.
[in]	gnss_signal	A boolean flag indicating if the GNSS velocity measurement in z[1] is valid (true) or not (false).

Returns

None

Definition at line 49 of file kalmanFilter.c.

{
  static const signed char b_a[4] = {1, 0, 0, 1};
  double F[4];
  double P0[4];
  double x_pred[2];
  double cos_alpha;
  double d;
  double d1;
  double d2;
  double d3;
  double d4;
  int a_tmp;
  int i;
  /*  Compute cos_alpha from the input tilt angle alpha */
  cos_alpha = cos(alpha);
  /*  State transition matrix */
  F[0] = 1.0;
  F[2] = Ts * cos_alpha;
  F[1] = 0.0;
  F[3] = 1.0;
  /*  Barometric altitude depends on vertical velocity component */
  /*  GNSS velocity has simple integration relationship */
  /*  Control input matrix */
  /*  Barometric altitude change */
  /*  GNSS velocity change */
  /*  Prediction step */
  x_pred[0] =
      (x_est[0] + x_est[1] * F[2]) + Ts * Ts / 2.0 * (a_m * cos_alpha - 9.81);
  x_pred[1] = (0.0 * x_est[0] + x_est[1]) + Ts * (a_m - 9.81 * cos_alpha);
  /*  Observation matrix - identity when both measurements available */
  /*  Always measure barometric altitude */
  /*  GNSS velocity measurement depends on signal */
  /*  Modify measurement update based on GNSS signal availability */
  if (gnss_signal == true) {
    double K[4];
    double a[4];
    double b_Ts[2];
    double P0_idx_0;
    double P0_idx_1;
    double P0_idx_2;
    double P0_idx_3;
    int b_a_tmp;
    /*  Full update (both altitude and velocity) */
    for (i = 0; i < 2; i++) {
      a_tmp = b_a[i];
      b_a_tmp = b_a[i + 2];
      cos_alpha = (double)a_tmp * P[0] + (double)b_a_tmp * P[1];
      d = (double)a_tmp * P[2] + (double)b_a_tmp * P[3];
      P0[i] = (cos_alpha + d * 0.0) + R[i];
      P0[i + 2] = (cos_alpha * 0.0 + d) + R[i + 2];
      cos_alpha = P[i + 2];
      a[i] = P[i] + cos_alpha * 0.0;
      a[i + 2] = P[i] * 0.0 + cos_alpha;
    }
    cos_alpha = P0[0] * P0[3] - P0[1] * P0[2];
    P0_idx_0 = P0[3] / cos_alpha;
    P0_idx_2 = -P0[2] / cos_alpha;
    P0_idx_1 = -P0[1] / cos_alpha;
    P0_idx_3 = P0[0] / cos_alpha;
    cos_alpha = P[0];
    d = P[1];
    d1 = P[2];
    d2 = P[3];
    d3 = x_pred[0];
    d4 = x_pred[1];
    for (i = 0; i < 2; i++) {
      double d5;
      double d6;
      double d7;
      d5 = a[i + 2];
      d6 = a[i];
      d7 = d6 * P0_idx_0 + d5 * P0_idx_1;
      K[i] = d7;
      d5 = d6 * P0_idx_2 + d5 * P0_idx_3;
      K[i + 2] = d5;
      a_tmp = b_a[i];
      d6 = (double)a_tmp - (d7 + d5 * 0.0);
      a[i] = d6;
      b_a_tmp = b_a[i + 2];
      d5 = (double)b_a_tmp - (d7 * 0.0 + d5);
      a[i + 2] = d5;
      P0[i] = d6 * cos_alpha + d5 * d;
      P0[i + 2] = d6 * d1 + d5 * d2;
      b_Ts[i] = z[i] - ((double)a_tmp * d3 + (double)b_a_tmp * d4);
    }
    x_est[0] = x_pred[0] + (K[0] * b_Ts[0] + b_Ts[1] * K[2]);
    x_est[1] = x_pred[1] + (b_Ts[0] * K[1] + b_Ts[1] * K[3]);
  } else {
    double a[4];
    /*  Partial update (only altitude) */
    /*  Only observe altitude */
    /*  Only altitude measurement noise */
    x_est[0] = P[0] + P[2] * 0.0;
    x_est[1] = P[1] + P[3] * 0.0;
    cos_alpha =
        1.0 / (((P[0] + 0.0 * P[1]) + (P[2] + 0.0 * P[3]) * 0.0) + R[0]);
    x_est[0] *= cos_alpha;
    x_est[1] *= cos_alpha;
    a[0] = 1.0 - x_est[0];
    a[1] = 0.0 - x_est[1];
    a[2] = 0.0 - x_est[0] * 0.0;
    a[3] = 1.0 - x_est[1] * 0.0;
    /*  Only update altitude (first element of state vector) */
    cos_alpha = 0.0;
    d = P[0];
    d1 = P[1];
    d2 = P[2];
    d3 = P[3];
    for (i = 0; i < 2; i++) {
      double d5;
      d4 = a[i + 2];
      d5 = a[i];
      P0[i] = d5 * d + d4 * d1;
      P0[i + 2] = d5 * d2 + d4 * d3;
      cos_alpha += (1.0 - (double)i) * x_pred[i];
    }
    cos_alpha = z[0] - cos_alpha;
    x_est[0] = x_pred[0] + x_est[0] * cos_alpha;
    x_est[1] = x_pred[1] + x_est[1] * cos_alpha;
  }
  /*  Always update covariance matrix */
  cos_alpha = P0[0];
  d = P0[1];
  d1 = P0[2];
  d2 = P0[3];
  for (i = 0; i < 2; i++) {
    d3 = F[i + 2];
    a_tmp = (int)F[i];
    d4 = (double)a_tmp * cos_alpha + d3 * d;
    d3 = (double)a_tmp * d1 + d3 * d2;
    P[i] = (d4 + d3 * F[2]) + Q[i];
    P[i + 2] = (d4 * 0.0 + d3) + Q[i + 2];
  }
}

References a_m, alpha, Q, R, Ts, x_est, and z.

Referenced by StartKalman_mkf().

Here is the caller graph for this function: